Java Quiz | Software Testing Material
Welcome to your %QUIZ_NAME%. This quiz consists of 25 multiple-choice questions. There is no negative marking in this. Click on NEXT button to Start this Java Quiz.
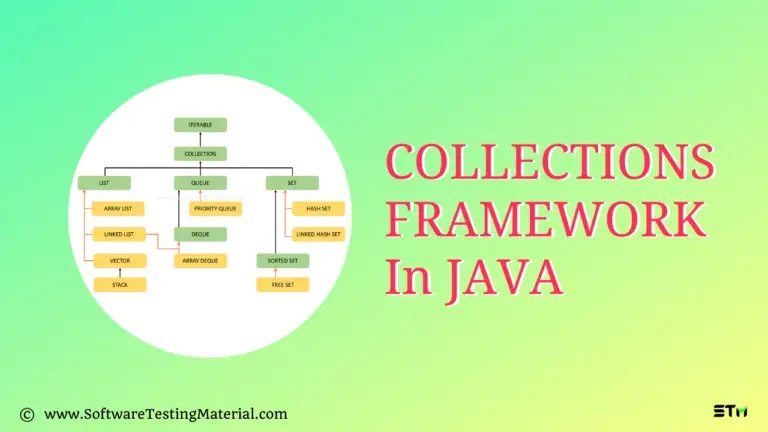
Java Quiz – You can test your knowledge with this Java Quiz. We have created this Java Quiz Online Test to help you master Java.
Knowledge Base: